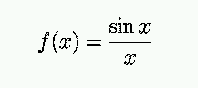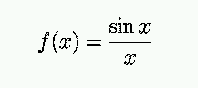Hints on Plotting the Function of the Week : Week 0, Hilary 1999

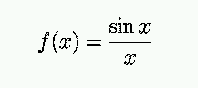
• f is even (ie, symmetrical about the y-axis), since sin(x) and x are both odd.
• f looks a bit like sin(x), but its amplitude is scaled by a factor of x.
• To see what f looks like at x = 0, do a Taylor expansion to see sin(x) = x + x^3/3! + ... and thus that sin(x)/x = 1 + x^2/3! + ..., so f(0) = 1.
• Work out df/dx, and note that it's zero if and only if tan(x) = x; so there are an infinite number of turning points, one of which is at zero, and which approach x = +/-(2n+1)pi/2 (n integer) as x tends to +/- infinity.
• Note f = 0 if and only if sin(x) = 0, ie at x = +/-n.pi (n integer), and these are also the places where the second derivative of f is zero, so they are also points of inflection.
• When sin(x) = 1, f(x) = 1/x; so at x = +/-(2n+1)pi/2 (n integer), f(x) lies on the line y = 1/x.

See the plot.

12 January 1999